Производная профессии что это
Опубликовано: 02.10.2024
Роль математики в различных областях естествознания очень велика. Недаром говорят «Математика – царица наук, физика ее правая рука, химия – левая».
Предмет исследования – производная.
Ведущая цель - показать значимость производной не только в математике, но и в других науках, её важность в современной жизни.
Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.
Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.
Ключевой и тематический вопросы данного реферата:
1. История возникновения производной.
2. Зачем изучать производные функций?
3. Где используются производные?
4. Применение производных в физике, химии, биологии и других науках.
Я решила написать работу на тему «Применение производной в различных областях науки», потому что считаю эту тему очень интересной, полезной и актуальной.
В своей работе я расскажу о применении дифференцирования в различных областях науки, таких как химия, физика, биология, география и т. д. Ведь все науки неразрывно связаны между собой, что очень хорошо видно на примере рассматриваемой мною темы.
Применение производной в различных областях науки
Из курса алгебры старших классов мы уже знаем, что производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.
Действие нахождения производной называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.
Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.
Ньютон ввел понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
Физический смысл производной: производная функции y = f ( x ) в точке x 0 – это скорость изменения функции f ( x ) в точке x 0 .

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.
Геометрический смысл производной состоит в том, что производная функция в точке x 0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x 0 .
Термин производная и современные обозначения y ' , f ' ввёл Ж.Лагранж в 1797г.
Российский математик 19 века Панфутий Львович Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека, например, как располагать своими средствами для достижения наибольшей выгоды».
С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:
Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;
Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;
Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.
При изучении любой темы у учеников возникает вопрос: «Зачем нам это надо?» Если ответ удовлетворит любопытство, то можно говорить о заинтересованности учеников. Ответ для темы «Производная» можно получить, зная, где используются производные функций.
Чтобы ответить на этот вопрос, можно перечислить некоторые дисциплины и их разделы, в которых применяются производные.
Производная в алгебре:
1. Касательная к графику функции 
Касательная к графику функции f, дифференцируемой в точке x о , - это прямая, проходящая через точку (x о ; f (x о )) и имеющая угловой коэффициент f ′(x о ).
y = f (x о ) + f ′(x о ) (x – x о )
2. Поиск промежутков возрастания и убывания функции
Функция y=f(x) возрастает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Функция y=f(x) убывает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

3. Поиск точек экстремума функции
Точку называют точкой максимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают .
Точку называют точкой минимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .
Под окрестностью точки понимают интервал , где - достаточно малое положительное число.
Точки минимума и максимума называют точками экстремума , а значения функции, соответствующие точкам экстремума, называют экстремумами функции .

4. Поиск промежутков выпуклости и вогнутости функции
График функции , дифференцируемой на интервале , является на этом интервале выпуклым , если график этой функции в пределах интервала лежит не выше любой своей касательной (рис. 1).
График функции , дифференцируемой на интервале , является на этом интервале вогнутым , если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).

Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.
5. Поиск точек изгиба функции

Производная в физике:
1. Скорость как производная пути 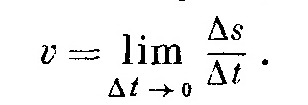
2. Ускорение как производная скорости a =
3. Скорость распада радиоактивных элементов = - λN
А так же в физике производную применяют для вычисления:
Скорости материальной точки
Мгновенной скорости как физический смысл производной
=
– мгновенная скорость, м/с
– перемещение тела, м ( если Δt→0 )
Δt – стремящийся к нулю интервал времени, с
Мгновенное значение силы переменного тока
Мгновенное значение ЭДС электромагнитной индукции
Максимальную мощность
Производная в химии:
И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.
Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности. V (t) = p ‘(t)
Темы исследований
Оформление работы
Наш баннер
Исследовательские работы и проекты
Производная в экономике

В процессе выполнения индивидуальной исследовательской работы по экономике "Производная в экономике" автором была поставлена цель, проинформировать учащихся об использовании производной в экономике. Для этого автор изучает свойства производной и дает полное определение понятия производной.
Подробнее о работе:
Результатом работы над ученическим проектом по экономике "Производная в экономике" стал разработанный учащейся справочник, с помощью которого можно будет легко и быстро вспомнить что такое производная и как она применяется в экономической сфере. В работе предложены примеры основных экономических задач, которые решаются с помощью производной. Полный текст проекта с формулами прикреплен внизу этой страницы.
Оглавление
Введение
1. История появления производной.
2. Понятие производной.
3. Сферы применения производной.
4. Производная в экономике.
Заключение
Информационные источники
Введение
Математика является не только орудием количественного расчета, но также методом точного исследования. Она служит средством предельно четкой и ясной формулировки экономических понятий и проблем.
Экономические задачи достаточно сложны, и чтобы облегчить решения данных задач, существует такое понятие, как «производная». В своей работе я попыталась объяснить и доказать, что производная действительно помогает решать различные экономические задачи.
Цель проекта: Проинформировать учащихся об использовании производной в экономике.
- Изучить свойства и понятия производной.
- Изучить возможности использования её в экономике.
- Создать справочник о производной и ее применении.
- Презентовать справочник учащимся.
Методы исследования: изучение различных интернет ресурсов и литературы.
Продукт проекта: справочник.
Предполагаемая аудитория реализации: 11 классы.
Срок реализации: 3 месяца.
Практическая значимость проекта: Практическая значимость проекта заключается в том, что с помощью справочника можно будет легко и быстро вспомнить что такое производная и как она применяется в экономической сфере.
В экономической сфере не редко приходится прибегать к различным графикам вычислениям и т.д. И не всегда это бывает легко так как со временем что то все равно забывается. Я выбрала эту тему так как она мне понравилась я захотела в ней разобраться получше и узнать каким образом производна помогает в экономике.
История появления производной
Это открытие Ньютона стало поворотным пунктом в истории естествознания. Честь открытия основных законов математического анализа наравне с Ньютоном принадлежит немецкому математику Готфриду Вильгельму Лейбницу.
К этим законам Лейбниц пришел, решая задачу проведения касательной к произвольной кривой, т.е. сформулировал геометрический смысл производной, что значение производной в точке касания есть угловой коэффициент касательной или tg угла наклона касательной с положительным направлением оси ОX.
Понятие производной
При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f (x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f (x). Тот процесс, с помощью которого из данной функции f (x) получают новую функцию f ' (x), называют дифференцированием и состоит он из следующих трех шагов:
2) составляем отношение
Определение: Производной y'=f '(x) данной функции y=f (x) при данном x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если, конечно, этот предел существует, т. е. конечен.
Сферы применения производной
В физике с помощью производной находится сила, мощность масса тонкого стержня, сила тока, скорость и ускорение, теплоёмкость.
В химии и естествознании для нахождения дозы лекарства, при которой побочный эффект будет минимальным, а реакция максимальной.
В военном деле в задачах о преследовании.
В сельском хозяйстве для определения рационального соотношения сторон прямоугольника, являющихся основой сети полевых работ.
Далее в проекте я разберу применение производной в экономике.
Производная в экономике
Производная в экономике решает важные вопросы:
- В каком направлении изменяется доход государства при увеличении налогов или при введении налоговых пошлин?
- Увеличивается или уменьшается выручка фирмы при повышении цены на её продукцию?
Если спросить экономиста “Что такое производная?”, то он ответит: «маржинализм». Слово «маржинализм» охватывает целый комплекс понятий в современной экономической науке.
"Marginal" в переводе с английского языка означает "находящийся на самом краю", "предельный", "граничный". К предельным величинам в экономике относятся: предельные издержки, предельный доход, предельная полезность, предельная производительность, предельная склонность к потреблению и т.д.
Понятие предельных величин позволило создать совершенно новый инструмент исследования и описания экономических явлений, посредством которого стало возможно решать научные проблемы, прежде не решённые или решённые неудовлетворительно. Все эти величины самым тесным образом связаны с понятием производной. Предельные величины характеризуют не состояние (как суммарная или средняя величины), а процесс, изменение экономического объекта. Следовательно, производная выступает как скорость изменения некоторого экономического объекта (процесса) с течением времени или относительно другого исследуемого фактора.
Конечно, экономика не всегда позволяет использовать предельные величины в силу неделимости многих экономических расчетов, а также прерывности (дискретности) экономических показателей во времени (например, годовых, квартальных, месячных и т.д.). В то же время во многих случаях можно эффективно использовать предельные величины.
Какое же отношение экономика имеет к производной?
Для ответа на этот вопрос рассмотрим следующую ситуацию:
Пусть предприятие «А» производит Х единиц продукции.
К - суммарные затраты или издержки производства.
Производственная функция, описывающая зависимость затрат от объёма производства имеет вид: К=f(х).
Теперь рассмотрим понятие предельных издержек производства:
Предельные издержки производства – это дополнительные затраты, которые несёт предприятие при увеличении объёма производства на бесконечно малую величину.
А это не что иное, как предел среднего приращения затрат при стремлении к нулю.
Так вычисляется значение производной функции в точке.
И получается мы получили не что иное, как ещё одно понятие производной, а точнее её экономический смысл.
Значение производной функции в данной точке есть предельные издержки производства при данном его объёме.
Таким образом у нас появилась ещё одна трактовка понятия производной к уже имеющимся.
Экономические задачи с производной
Задача № 1.
Пусть функция затрат при производстве апатитового концентрата имеет вид:
Определить предельные издержки производства при увеличении объёма выпуска на х1 = 2ед. и на х2= 10ед.
7
1. Предельные издержки это рост затрат при увеличении объёма производства на 2 ед. и на 10 ед.
2. Но предельные издержки это ещё и значение производной функции в точке.
3. предельные издержки производства составляют 2,5 ден.ед. при росте объёма производства на 2 ед. и 2,17 при росте объёмов производства на 10 ед.
Вопрос: выгодно ли данному предприятию наращивать производство, если уровень затрат не изменится?
Вывод: с ростом производства затраты на каждую следующую единицу продукции уменьшаются, следовательно, в данном случае увеличивать объём производства выгодно.
Задача № 2.
Предприятие производит Х единиц продукции.
Установлено, что зависимость финансовых накоплений от объёма выпуска задаётся формулой.
Определить максимально возможную величину финансовых накоплений.
Вопрос: переведите экономический вопрос задачи на математический язык, или др. словами составьте математическую модель данной задачи.
Ответ: необходимо найти наибольшее и наименьшее значение функции.
1) Из экономического смысла переменной определяем, что она должна быть неотрицательной.
Вывод: финансовые накопления предприятия растут при увеличении объёма производства до100 единиц, достигая суммы 39000 ден. единиц.
Вопрос: выгодно ли наращивать объёмы производства при неизменных прочих условиях?
Ответ: дальнейший рост производства нецелесообразен, т.к. он приведёт к сокращению финансовых накоплений.
Задача № 3.
Цементный завод производит X тонн цемента в день. По договору н должен ежедневно поставлять строительной фирме не менее 20 тонн цемента. Производственные мощности завода таковы, что выпуск не может превышать 90 тонн в день.
Определить: 1) при каком объёме производства удельные затраты производства будут наибольшими ( наименьшими);
2) выгодно ли строительной фирме быть единственным партнёром завода.
Вывод: 1) наибольшая величина затрат на единицу продукции составит 2601ден.единицу при выпуске 49 тонн цемента в день , а наименьшая 920 ден. единиц при выпуске 90 тонн цемента в день.
2) фирме не выгодно быть единственным потребителем цемента, т.к. она переплачивает за товар.
Вопрос: каковы должны быть ближайшие шаги руководства заводом?
Ответ: срочный поиск новых потребителей, иначе завод рискует потерять и тех клиентов, которых имеет.
Я хотел подзаработать на продаже газет. На соседнем углу дневной спрос- прямая линия. При этом если цена газеты 12,5 рублей, то газеты не берут вовсе, а больше 50 газет продать не удаётся никогда. Тётя Клава, которая работает в типографии, сказала, что даст мне столько газет, сколько надо за коробку конфет, а Витька, мой конкурент из параллельного класса, сказал, что даст мне 30 рублей, если я вовсе не появлюсь на том углу со своими газетами.
Стоит ли мне начинать продажу газет, если да, то, сколько газет просить, и по какой цене продавать?
1) Определим функцию спроса, т.е. определим, по какому закону продаются газеты.
График уравнения, описывающего закон продаж должен проходить через точки (12,5 ; 0) и (0 ; 50), значит это будет линейная зависимость.

- при Р = 0 , а Q = 50 получаем, что k*0+b= 50, значит b=50.
- при P = 12,5, а Q= 0 получаем, что 12,5 k+ 50 = 0, значит k = -4
- объём продаж будет выражаться формулой: Q(P) = - 4P+ 50
2) По условию задачи бизнес следует начинать если прибыль будет наибольшей, значит нам следует найти наибольшую величину прибыли ( выручки).
3) Обозначим прибыль через R(P).
4) Найдём наибольшее значение выручки на промежутке (0, 12,5)
Вопрос: мы ответили на вопрос задачи о прибыли от бизнеса?
Ответ: нет, т.к. мы не приняли в расчёт тётю Клаву с её коробкой конфет, а это величина наших затрат, которая повлияет на прибыль.
Итак: начинать бизнес следует, если прибыль от него будет выше суммы предложенной Витькой (альтернативный доход), с учётом купленной коробки конфет.
Если цена конфет будет выше 156.25-30=126,25 рублей, то дело не будет выгодно.
Вывод: бизнес следует начинать, если цена коробки конфет будет меньше 126, 25 р., брать25 газет и продавать по 6,25р.

Знания, получаемые студентами в процессе изучения дисциплин профессионального цикла, должны использоваться ими для выявления определенных математических закономерностей в различных производственных процессах. Это достигается с помощью профессиональной направленности в преподавании математики, наиболее распространенной формой которой является решение задач с производственным содержанием. В данной работе предлагается система задач по теме "Производная и её применение".
| Вложение | Размер |
|---|---|
| prof_napravl.doc | 225 КБ |
Предварительный просмотр:
ПРОФЕССИОНАЛЬНАЯ НАПРАВЛЕННОСТЬ ИЗУЧЕНИЯ ТЕМЫ
« ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
В КОЛЛЕДЖАХ ЭЛЕКТРОТЕХНИЧЕСКИХ ПРОФЕССИЙ»
Кировой Елены Анатольевны
- Вступление.
- Основная часть.
- Решение задач с производственным содержанием – одна из форм работы по осуществлению профессиональной направленности преподавания математики в колледжах.
- Решение прикладных задач при изучении темы «Производная и ее применение» в колледжах электротехнических профессий.
- Заключение.
Высокие темпы развития электротехнической, электроэнергетической, электронной промышленности предъявляют все возрастающие требования к подготовке квалифицированных рабочих по электротехническим и электроэнергетическим профессиям. В настоящее время большинство рабочих проходит профессиональную подготовку в системе профессионально-технического образования. Будущие рабочие должны овладеть не только общетехническими и специальными знаниями, но и получить серьёзную общеобразовательную подготовку.
Математические методы все более проникают в большинство областей человеческих знаний. Именно поэтому, среди общеобразовательных предметов, которые служат основой профессиональной подготовки рабочих электротехнических специальностей, одно из первых мест занимает математика, так как изучение таких предметов, как электротехника и радиоэлектроника, которые входят в профессионально-технический цикл обучения, невозможно без хорошей математической подготовки. Обучение математике в средних профессионально- технических колледжах вооружает учащихся определенными знаниями, умениями и навыками, необходимыми для их практической деятельности в условиях современного производства, достижения такого уровня их математической развития, который необходим для изучения других предметов и продолжения образования.
С другой стороны, знания, получаемые учащимися в процессе изучения предметов профессионально-технического цикла, должны использоваться ими для выявления определенных математических закономерностей в различных производственных процессах. Это достигается с помощью профессиональной направленности в преподавании математики, наиболее распространенной формой проявления которой является решение задач с производственным содержанием.
§1. Решение задач с производственным содержанием – одна из форм работы по осуществлению профессиональной направленности преподавания математики в средних профессиональных колледжах
На уроках математики необходимо органическую связь изучаемого теоретического и задачного материала, формировать у учащихся прочные и осознанные математические навыки, необходимые как для дальнейшего изучения математики, решения прикладных задач. Важное значение в процессе обучения математике имеет понимание учащимися практической значимости того или иного учебного материала, ближней и дальней перспективы его использования.
Использования математики для решения любой практической задачи предусматривает три этапа:
- переход от ситуации, которою необходимо разрушить, к формальной математической модели;
- решение этой задачи методами математики;
- проверка применения этого решения к исходной ситуации и сопоставление решений с ней.
Содержание упражнений и задач по математике рассматривается в основном на втором этапе, то – есть учащимся предлагаются задачи, уже сформулированные на языке математике. В системе профессионально – технического образования желательно прикладная ориентация преподавания математике.
Среди требований к задачам по математике с производственным содержанием, в первую очередь, следует выделить требования к тому, чтобы связь математики с производственным материалом выражалось по существу, а не нужным формального привлечения производственных терминов.
Следует отметить, что иногда в так называемых задачах с производственным содержанием предусматривается вычисление практически ненужных величин. Задача с производственным содержанием должна иметь целенаправленный характер, чтобы учащимся была понятна практическая необходимость ее решения.
Решение задач с производственным содержанием могут быть предложены учащимся на различных этапах обучения. Решение задач на этапах восприятия и осмысления нового материала имеет целью пробудить у учащихся потребность в расширении знаний, познавательный интерес и научить их методам самостоятельного приобретения знаний. Решая и анализируя задачи на этапах закрепления и повторения учебного материала, учащиеся овладевают способами применения знаний на практике и вместе с тем более глубоко усваивают его содержание. При проверке усвоения программного материала решение задач с производственным содержанием позволяет установить, насколько прочно и глубоко его усвоили.
§2. Решение прикладных задач при изучении темы
«Производная и ее применение» в электротехнической профессии
Обучение в колледжах требует, чтобы при преподавании элементов математического анализа обеспечивалось органическое единство изложения теории и практики, развивающее у учащихся умение применять теорию для решения прикладных задач. Изучая элементы математического анализа, учащиеся должны усвоить и оценить их прикладные возможности и получить основные навыки в применении элементов математического анализа при решении практических задач.
Именно через специально составленную систему задач можно показать применение математических знаний для познания реального мира, познакомить учащихся с методами решения задач в науке и практической деятельности. При решении прикладных задач формируются профессиональные интересы учащихся, так как при этом они знакомятся с применением математических знаний в производстве.
Опыт показывает, что относительно нетрудно научить учащихся формулировать определение производной, вычислять производную, находить производную в точке, пользуясь основными правилами дифференцирования и применять её в тех случаях, когда учащимся заранее известен алгоритм решения. Не вызывает особых затруднений и алгоритм применения производной при исследовании функций не экстремум. Гораздо труднее добиться того, чтобы учащиеся научились самостоятельно видеть производную в различных её частных проявлениях. Ведь очень многие понятия естественных наук не только не могут быть количественно охарактеризованы без понятия производной, но даже не могут быть без неё определены.
Раздел «Производная и её применение» начинается с изучения средней скорости изменения функции на некотором промежутке и понятия о пределе средней скорости изменения функции в точке, то есть производной в точке.
Введению понятия производной функции предшествует рассмотрение некоторых прикладных задач. Такими задачами являются, например, задачи о мгновенной величине тока; о ЭДС самоиндукции, возникающей в некоторый момент времени.
Напряжение на конденсаторе ёмкостью C изменяется по закону U(t) . Найти ток, проходящий через конденсатор в момент времени t, если емкость конденсатора определяется по формуле , где q значение заряда одной из обкладок.
За время с момента t до момента t + Δt через конденсатор пройдёт количество электричества Δq . Среднее значение тока за интервал времени Δt равно .
Пусть в некоторый момент времени t напряжение на конденсаторе U(t) , а протекающий через него ток равен i(t).
Тогда значение заряда на одной из обкладок q (t) = C ∙U(t) .
В момент времени t + Δt напряжение равно U ( t + Δt) , а заряд q (t + Δt) = C ∙U(t + Δt) .
Таким образом, за время Δt через конденсатор пройдёт количество электричества, равное
Δq = q(t + Δt) – q(t) = C ∙ U(t + Δt) – U(t).
Следовательно, среднее значение тока, протекающее через конденсатор за время Δt , составит .
Полагая, что , получим мгновенную величину тока при t как предел среднего значения тока.
Ток, проходящий через катушку с индуктивностью L , изменяется по закону i (t) .
Найти ЭДС самоиндукции, возникающей в катушке в момент t , если индуктивность катушки определяется по формуле , где Ф – магнитный поток, создаваемый катушкой, имеющей w витков, а среднее значении ЭДС самоиндукции за время Δt равно , где ΔФ – изменение магнитного потока за это время .
Пусть в некоторый момент времени t ток, проходящий через катушку, равен i(t) , а ЭДС самоиндукции, возникающая в катушки l(t) .
Тогда магнитный поток, создаваемый катушкой будет равен .
В момент времени t + Δt ток равен i (t + Δt) , а магнитный поток .
Таким образом, за время Δt магнитный поток изменяется на величину .
Это изменение магнитного потока приведет к появлению в катушке ЭДС самоиндукции, среднее значение которой за время Δt равно: .
Тогда при получим ЭДС самоиндукции в катушке в момент t :
Опыт показывает, что учащиеся без труда осваивают технику дифференцирования.
Однако это может заслонить от них смысл производной и широкие возможности её практического применения. Поэтому рассматриваемые упражнения, не требующие при их выполнении сложной техники дифференцирования, способствуют дальнейшему формированию понятия производной. Чередуя их с чисто вычислительными упражнениями можно добиться устойчивого интереса к данной теме.
В схеме, состоящей из последовательного соединения резистора и конденсатора, напряжение на конденсаторе поддерживается постоянным. Найти ток в цепи.
Найдите изменение ЭДС самоиндукции, возникающей в катушке с индуктивностью L , если ток, проходящий через катушку изменяется по закону:
В какие моменты времени ток в цепи равен нулю, если количество электричества, протекающего через проводник, задаётся формулой ?
Основой разнообразных физических приложений производной является понятие дифференциала.
Приращение функции отличается от ее дифференциала на такую функцию, которая стремится к нулю еще быстрее, чем Δх.
Для вычисления дифференциала в физике достаточно знать, что дифференциал – это главная часть приращения функции, линейно зависящая от приращения аргумента.
Найти приращение тока, протекающего через резистор сопротивлением 100 Ом при напряжении 10В, если сопротивление увеличивается на 10 Ом, а напряжение поддерживается постоянным.
Закон Ома для участка цепи
Таким образом, ток уменьшается на .
Найти погрешность вычисления энергии заряженного конденсатора, если емкость конденсатора С =10мкФ, а напряжение U=12,2В измерено с погрешностью 0,1В.
Энергия W конденсатора между его обкладками: .
Очень важен в прикладном аспекте материал, связанный с нахождением наибольшего и наименьшего значений функции. Формирование умений решать такие задачи – одна из важнейших целей изучения начал математического анализа. Задачи этого типа имеют четкую прикладную направленность. В них есть все фазы построения и использования математической модели.
Источник напряжения с ЭДС Е = 200В и внутренним сопротивлением r =100 Ом замкнут на реостат. При каком токе мощность во внешней цепи будет максимальной?
Мощность во внешней цепи равна P = U∙J
Закон Ома для полной цепи:
, где r - внутреннее сопротивление, R - сопротивление нагрузки
Найдем производную функции P(J) и приравняем ее к нулю:
Найдем знак в точках и .
В точке знак производной меняется с «+» на «–».
Следовательно, при токе .
Мощность во внешней цепи принимает максимальное значение и равна:
Элемент, ЭДС которого Е и внутреннее сопротивление r, замкнут на внешнее сопротивление R. Наибольшая мощность во внешней цепи P = 9Вт; а сила тока J= 3А. Найти величины E и r .
Используя результаты примера 8, имеем ,
Можно составить систему уравнений относительно Е и r:
Ответ: Е = 6В, r =1Ом
Через алюминиевую шину прямоугольного сечения длины l пропускают ток силой 160A и плотностью . Чтобы шина не перегрелась, теплоотдача должна быть как можно больше, т.е. шина должна быть боковую поверхность. Найти размеры сечения шины, при которых боковая поверхность шины максимальна, если по конструктивным соображениям требуется, чтобы толщина шины заключалась в пределах от 4 до 8 мм.
Плотность электрического тока в проводнике с током J определяется по формуле , где S – площадь сечения проводника,
Пусть ширина шины, её толщина.
Площадь боковой поверхности шины:
Найдем производную функции S б (у) и приравняем ее к нулю:
Т.к. у – толщина шины, следовательно .
Найдем знак в точках и .
По условию задачи , .
Тогда функция S б (у) достигает наибольшее значение в одной из граничных точек, т.е.
в точках у = 4 или у = 8 . На интервале принимает отрицательное значение, следовательно функция S б (у) монотонно убывает на этом интервале. Максимальное значение функция S б (у) достигает в точке у = 4 .
Ответ: толщина шины 4мм, ширина шины 40мм.
При каком коэффициента трансформации k напряжение U между зажимами трехфазного трансформатора будет минимальным, если ,
где U 0 – напряжение, под которые включаются обмотки трансформатора.
Точка является точкой минимума функции .
В учебных пособиях по математике, по которым ведется преподавание колледжах не всегда учтена специфика обучения, заключающаяся в одновременной образовательной и профессиональной подготовке учащихся. Осуществление более тесной связи преподавания математики с профессиональной деятельностью позволит предать изучению математики профессиональную направленность, а формирование профессиональных знаний и умений проводить с опорой на имеющуюся математическую подготовку учащихся.
Изучение планов и программ по спецпредметам, посещение уроков производственного обучения, освоение производственной терминологии, совместная работа с мастерами производственного обучения и преподавателями спецдисциплин по составлению межпредметных задач и упражнений – вот основные поиски путей осуществления профессиональной направленности преподавания математики.
Профессиональная направленность в процессе обучения элементам математического анализа эффективно осуществляется через специально составленную систему задач с производственным содержанием. Наблюдения за отношением учащихся к содержанию таких задач показывают, что содержание учебной задачи, метод решения которой освоен учащимися, вызывает у них интерес. Такие учебные задачи становятся средством формирования интереса к профессии. Прикладные задачи повышают интерес учащихся и к самой математике, поскольку для большинства учащихся ценность математического образования состоит в ее практических возможностях. Однако, удачный подбор содержательных практических задач еще не обеспечивает должного эффекта. Такие задачи, как правило, вызывают у учащихся затруднения. Условие прикладной задачи только тогда легко доходит до сознания учащихся, когда они встречались с описываемой ситуацией в реальной действительности. Поэтому при постановке производственных задач следует широко опираться на наглядные аналоги из производственного окружения, на трудовой опыт учащихся.
Умение решать прикладные задачи, так же как и руководить их решением, приходит с опытом, при систематическом использовании таких задач в учебном процессе.
По теме: методические разработки, презентации и конспекты
Предлагаю интересный материал по русскому языку для использования на уроках и для самостоятельной работы студентов медицинского колледжа. Предусматривается работа со справочными медицинскими изданиями.

Методические указания для обучающихся по изучению профессионального модуля 06 Выполнение работ по одной или нескольким профессиям рабочих, должностям служащих
Методические указания для обучающихся по организации изучения профессионального модуля 06 Выполнение работ по одной или нескольким профессиям рабочих, должностям служащих/ Сост.: Н.И.Демченко. – Брянс.
Преподавание дисциплины «Индивидуальный учебный проект» с учетом профессиональной направленности обучающихся.Профессиональная, практическая и социальная направленность проектной деятельности обу.
В материале изложена авторская позиция изучения вопроса мотивированности в профессиональном самоопределении обучающихся СПО.

Использование лексики профессиональной направленности при изучении БД.01 Русский язык в СПО.
Как использовать лексику профессиональной направленности на занятиях русского языка в группах 1 курса.

Школа педагогического роста, как одно из направлений профессионального развития педагогов в ГАПОУ ТО «Тюменский колледж водного транспорта»
Статья. Соавтор - Важнова Е.Р., зам. директора колледжа по учебно-методической работе.
Интеграция действительно актуальна в наше время. В условиях кардинальных изменений, происходящих во всех сферах жизни и деятельности общества, интеграции России в мировое сообщество, интеграционных пр.
Когда-то в школе я не понимал производных. Не подумайте, что я был совсем уж дураком — я знал определение, умел их брать (в рамках простеньких школьных примеров) и оценки по математике имел неплохие.
Но вот смысл этого понятия от меня ускользал. Я понимал насколько важен график некоторой функции — по нему легком можно увидеть зависимость функции от аргумента. Глянул в какую-нибудь точку — и сразу ясно положение дел в данном конкретном месте. И что с этого?
Смысл производной
Сложность подачи информации о производной заключается в том, что это одно из абстрактных понятий, физический смысл которых трудно представить наглядно. Если, например, численные величины, их сумму и произведение, возведение в степень несложно объяснить в понятиях окружающего мира (количество, площадь, объем и т.п.), то смысл производной зачастую ускользает от понимания школьников, поэтому они могут выполнять задачи на ее вычисление чисто механически по затверженным формулам.
Производная, как известно, характеризует скорость изменения функции в конкретной точке. Определение этого понятия звучит достаточно сложно:
«предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует».
Трудность понимания этого определения с точки зрения школьника можно охарактеризовать как «все слова по отдельности понятны, а общий смысл уловить не получается». Разумеется, без подробного и наглядного объяснения ученику останется лишь затучить эту фразу, не понимая ее смысла.
Как же понять смысл производной? Ниже -, простой пример из повседневной жизни.
Допустим, два ученика одного класса — назовем их Иванов и Петров — получили за контрольную работу по теме «Системы уравнений и неравенств» по оценке «четыре». При этом Иванов весьма доволен, а Петров опечален. Такое их отношение к оценке станет понятным, если мы будем знать, что Петров — круглый отличник, а Иванов ни разу не получал по математике выше «тройки».
То есть, если рассматривать их оценки в динамике, мы видим, что у Иванова наблюдается прирост успеваемости (функция растет, ее производная положительна), а у Петрова, напротив, падение (функция убывает, производная отрицательна). То есть конкретная оценка (точка на графике функции) отображает текущее положение дел, а производная (касательная к графику в этой функции) показывает нам тенденцию развития ситуации.
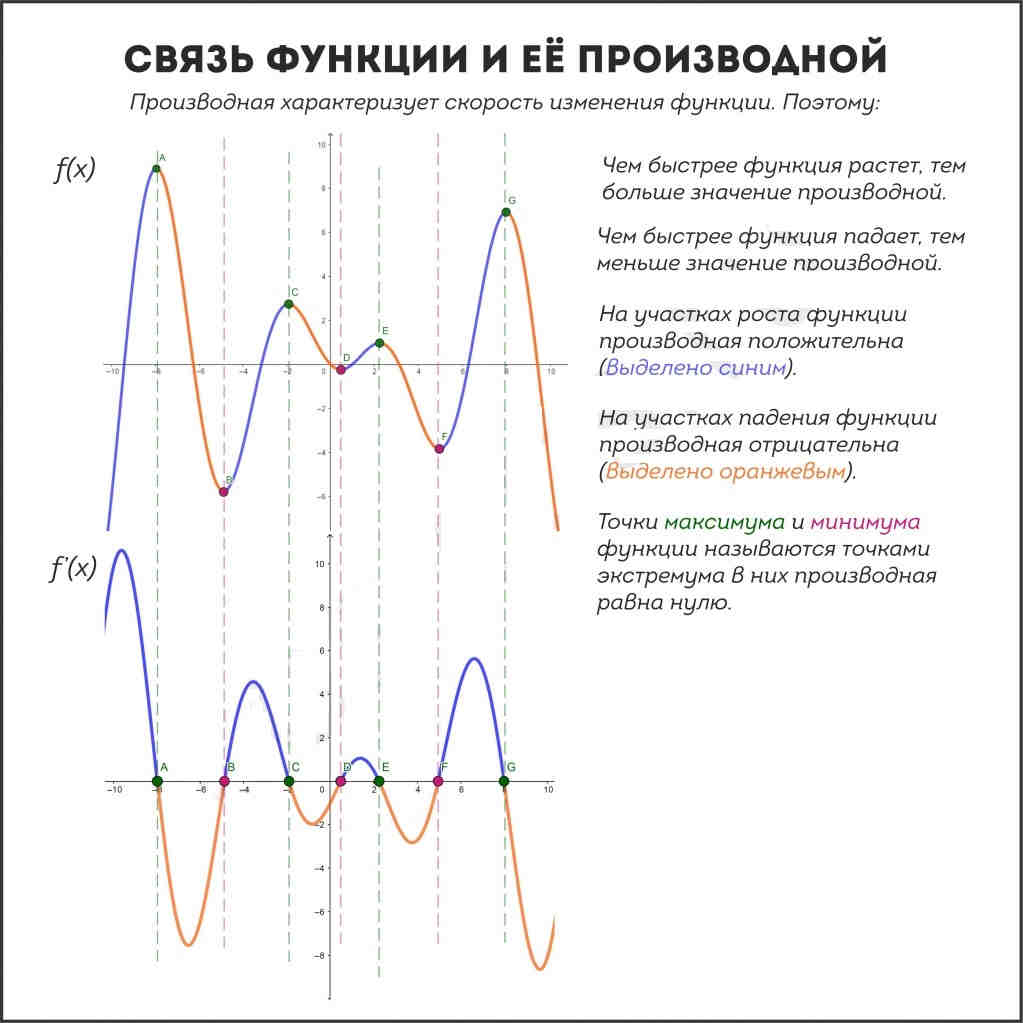
Аналогично в физике: движение тел характеризуется не только скоростью, но и ускорением, то есть тем, увеличивается или уменьшается ли его скорость. На этих или других подобных примерах можно пояснить, что производная — важнейшая характеристика именно динамики любых процессов, то есть она описывает закон, по которому изменяется мгновенное значение любой функции.
И чтобы вообще добить.
А что такое производная от производной?
Если мы берем какую-то физическую величину, и берем от нее производную, например, от времени, это означает скорость возрастания этой физической величины от времени. Простой пример: берем расстояние, которое прошел человек, выражаем ее какой-то формулой, берем производную от этой формулы по времени, получаем- угадайте что? Скорость этого человека! Но, очень важно упомянуть, что мы получаем скорость этого человека от времени.
Круто! Значит, если мы возьмем производную от скорости по времени, то мы получим скорость возрастания. Скорости? Ну, да, как-то так.
Лично я всегда понимал все гораздо проще на примерах, поэтому:
Идет человек ранним утром, и пьет кофе. Каждый раз, когда он выпивает глоток, то его скорость увеличивается, но увеличивается постепенно. Значит, его скорость растет, значит человек ускоряется.
Итак, в общем случае, физический смысл производной- скорость роста той или иной величины в зависимости от той величины, по которой мы берем эту самую производную. Если мы возьмем производную еще раз, получим скорость возрастания скорости и так далее. Все просто (наверное)
Темы исследований
Оформление работы
Наш баннер
Исследовательские работы и проекты
Производная в экономике

В процессе выполнения индивидуальной исследовательской работы по экономике "Производная в экономике" автором была поставлена цель, проинформировать учащихся об использовании производной в экономике. Для этого автор изучает свойства производной и дает полное определение понятия производной.
Подробнее о работе:
Результатом работы над ученическим проектом по экономике "Производная в экономике" стал разработанный учащейся справочник, с помощью которого можно будет легко и быстро вспомнить что такое производная и как она применяется в экономической сфере. В работе предложены примеры основных экономических задач, которые решаются с помощью производной. Полный текст проекта с формулами прикреплен внизу этой страницы.
Оглавление
Введение
1. История появления производной.
2. Понятие производной.
3. Сферы применения производной.
4. Производная в экономике.
Заключение
Информационные источники
Введение
Математика является не только орудием количественного расчета, но также методом точного исследования. Она служит средством предельно четкой и ясной формулировки экономических понятий и проблем.
Экономические задачи достаточно сложны, и чтобы облегчить решения данных задач, существует такое понятие, как «производная». В своей работе я попыталась объяснить и доказать, что производная действительно помогает решать различные экономические задачи.
Цель проекта: Проинформировать учащихся об использовании производной в экономике.
- Изучить свойства и понятия производной.
- Изучить возможности использования её в экономике.
- Создать справочник о производной и ее применении.
- Презентовать справочник учащимся.
Методы исследования: изучение различных интернет ресурсов и литературы.
Продукт проекта: справочник.
Предполагаемая аудитория реализации: 11 классы.
Срок реализации: 3 месяца.
Практическая значимость проекта: Практическая значимость проекта заключается в том, что с помощью справочника можно будет легко и быстро вспомнить что такое производная и как она применяется в экономической сфере.
В экономической сфере не редко приходится прибегать к различным графикам вычислениям и т.д. И не всегда это бывает легко так как со временем что то все равно забывается. Я выбрала эту тему так как она мне понравилась я захотела в ней разобраться получше и узнать каким образом производна помогает в экономике.
История появления производной
Это открытие Ньютона стало поворотным пунктом в истории естествознания. Честь открытия основных законов математического анализа наравне с Ньютоном принадлежит немецкому математику Готфриду Вильгельму Лейбницу.
К этим законам Лейбниц пришел, решая задачу проведения касательной к произвольной кривой, т.е. сформулировал геометрический смысл производной, что значение производной в точке касания есть угловой коэффициент касательной или tg угла наклона касательной с положительным направлением оси ОX.
Понятие производной
При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f (x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f (x). Тот процесс, с помощью которого из данной функции f (x) получают новую функцию f ' (x), называют дифференцированием и состоит он из следующих трех шагов:
2) составляем отношение
Определение: Производной y'=f '(x) данной функции y=f (x) при данном x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если, конечно, этот предел существует, т. е. конечен.
Сферы применения производной
В физике с помощью производной находится сила, мощность масса тонкого стержня, сила тока, скорость и ускорение, теплоёмкость.
В химии и естествознании для нахождения дозы лекарства, при которой побочный эффект будет минимальным, а реакция максимальной.
В военном деле в задачах о преследовании.
В сельском хозяйстве для определения рационального соотношения сторон прямоугольника, являющихся основой сети полевых работ.
Далее в проекте я разберу применение производной в экономике.
Производная в экономике
Производная в экономике решает важные вопросы:
- В каком направлении изменяется доход государства при увеличении налогов или при введении налоговых пошлин?
- Увеличивается или уменьшается выручка фирмы при повышении цены на её продукцию?
Если спросить экономиста “Что такое производная?”, то он ответит: «маржинализм». Слово «маржинализм» охватывает целый комплекс понятий в современной экономической науке.
"Marginal" в переводе с английского языка означает "находящийся на самом краю", "предельный", "граничный". К предельным величинам в экономике относятся: предельные издержки, предельный доход, предельная полезность, предельная производительность, предельная склонность к потреблению и т.д.
Понятие предельных величин позволило создать совершенно новый инструмент исследования и описания экономических явлений, посредством которого стало возможно решать научные проблемы, прежде не решённые или решённые неудовлетворительно. Все эти величины самым тесным образом связаны с понятием производной. Предельные величины характеризуют не состояние (как суммарная или средняя величины), а процесс, изменение экономического объекта. Следовательно, производная выступает как скорость изменения некоторого экономического объекта (процесса) с течением времени или относительно другого исследуемого фактора.
Конечно, экономика не всегда позволяет использовать предельные величины в силу неделимости многих экономических расчетов, а также прерывности (дискретности) экономических показателей во времени (например, годовых, квартальных, месячных и т.д.). В то же время во многих случаях можно эффективно использовать предельные величины.
Какое же отношение экономика имеет к производной?
Для ответа на этот вопрос рассмотрим следующую ситуацию:
Пусть предприятие «А» производит Х единиц продукции.
К - суммарные затраты или издержки производства.
Производственная функция, описывающая зависимость затрат от объёма производства имеет вид: К=f(х).
Теперь рассмотрим понятие предельных издержек производства:
Предельные издержки производства – это дополнительные затраты, которые несёт предприятие при увеличении объёма производства на бесконечно малую величину.
А это не что иное, как предел среднего приращения затрат при стремлении к нулю.
Так вычисляется значение производной функции в точке.
И получается мы получили не что иное, как ещё одно понятие производной, а точнее её экономический смысл.
Значение производной функции в данной точке есть предельные издержки производства при данном его объёме.
Таким образом у нас появилась ещё одна трактовка понятия производной к уже имеющимся.
Экономические задачи с производной
Задача № 1.
Пусть функция затрат при производстве апатитового концентрата имеет вид:
Определить предельные издержки производства при увеличении объёма выпуска на х1 = 2ед. и на х2= 10ед.
7
1. Предельные издержки это рост затрат при увеличении объёма производства на 2 ед. и на 10 ед.
2. Но предельные издержки это ещё и значение производной функции в точке.
3. предельные издержки производства составляют 2,5 ден.ед. при росте объёма производства на 2 ед. и 2,17 при росте объёмов производства на 10 ед.
Вопрос: выгодно ли данному предприятию наращивать производство, если уровень затрат не изменится?
Вывод: с ростом производства затраты на каждую следующую единицу продукции уменьшаются, следовательно, в данном случае увеличивать объём производства выгодно.
Задача № 2.
Предприятие производит Х единиц продукции.
Установлено, что зависимость финансовых накоплений от объёма выпуска задаётся формулой.
Определить максимально возможную величину финансовых накоплений.
Вопрос: переведите экономический вопрос задачи на математический язык, или др. словами составьте математическую модель данной задачи.
Ответ: необходимо найти наибольшее и наименьшее значение функции.
1) Из экономического смысла переменной определяем, что она должна быть неотрицательной.
Вывод: финансовые накопления предприятия растут при увеличении объёма производства до100 единиц, достигая суммы 39000 ден. единиц.
Вопрос: выгодно ли наращивать объёмы производства при неизменных прочих условиях?
Ответ: дальнейший рост производства нецелесообразен, т.к. он приведёт к сокращению финансовых накоплений.
Задача № 3.
Цементный завод производит X тонн цемента в день. По договору н должен ежедневно поставлять строительной фирме не менее 20 тонн цемента. Производственные мощности завода таковы, что выпуск не может превышать 90 тонн в день.
Определить: 1) при каком объёме производства удельные затраты производства будут наибольшими ( наименьшими);
2) выгодно ли строительной фирме быть единственным партнёром завода.
Вывод: 1) наибольшая величина затрат на единицу продукции составит 2601ден.единицу при выпуске 49 тонн цемента в день , а наименьшая 920 ден. единиц при выпуске 90 тонн цемента в день.
2) фирме не выгодно быть единственным потребителем цемента, т.к. она переплачивает за товар.
Вопрос: каковы должны быть ближайшие шаги руководства заводом?
Ответ: срочный поиск новых потребителей, иначе завод рискует потерять и тех клиентов, которых имеет.
Я хотел подзаработать на продаже газет. На соседнем углу дневной спрос- прямая линия. При этом если цена газеты 12,5 рублей, то газеты не берут вовсе, а больше 50 газет продать не удаётся никогда. Тётя Клава, которая работает в типографии, сказала, что даст мне столько газет, сколько надо за коробку конфет, а Витька, мой конкурент из параллельного класса, сказал, что даст мне 30 рублей, если я вовсе не появлюсь на том углу со своими газетами.
Стоит ли мне начинать продажу газет, если да, то, сколько газет просить, и по какой цене продавать?
1) Определим функцию спроса, т.е. определим, по какому закону продаются газеты.
График уравнения, описывающего закон продаж должен проходить через точки (12,5 ; 0) и (0 ; 50), значит это будет линейная зависимость.

- при Р = 0 , а Q = 50 получаем, что k*0+b= 50, значит b=50.
- при P = 12,5, а Q= 0 получаем, что 12,5 k+ 50 = 0, значит k = -4
- объём продаж будет выражаться формулой: Q(P) = - 4P+ 50
2) По условию задачи бизнес следует начинать если прибыль будет наибольшей, значит нам следует найти наибольшую величину прибыли ( выручки).
3) Обозначим прибыль через R(P).
4) Найдём наибольшее значение выручки на промежутке (0, 12,5)
Вопрос: мы ответили на вопрос задачи о прибыли от бизнеса?
Ответ: нет, т.к. мы не приняли в расчёт тётю Клаву с её коробкой конфет, а это величина наших затрат, которая повлияет на прибыль.
Итак: начинать бизнес следует, если прибыль от него будет выше суммы предложенной Витькой (альтернативный доход), с учётом купленной коробки конфет.
Если цена конфет будет выше 156.25-30=126,25 рублей, то дело не будет выгодно.
Вывод: бизнес следует начинать, если цена коробки конфет будет меньше 126, 25 р., брать25 газет и продавать по 6,25р.
Читайте также:

